By Ben Marsh, Sei Labs Research for Sei Research Initiative.

Introduction

One of the notable things about Autobahn, the consensus protocol used in the Sei Giga proof of concept, is the existence of concurrent rather than sequential block production. When a validator is creating a block they are doing so at the same time as other validators with those blocks being published on a public DA layer before a tip cut starts the consensus process. Between the lack of a traditional mempool and these public blocks the face of MEV in an Autobahn style chain looks a lot different.

The publicly visible transactions in blocks that have been published by one validator can be exploited by another validator exploiting last look advantages, running inter-block MEV attempting to front-run transactions in another block, or even just outright stealing a transaction from another block because they see a revenue opportunity if said transaction is present in their block.

Public DA

Autobahn, like some other modern consensus protocols, separates DA from consensus to remove DA from the critical path and target better bandwidth utilization and confirmation latency. Multiple blocks are proposed in concurrent gathering a \(f+1\) PoA certificate to be included in a tip cut every tick. This tip cut ultimately defines ordering of transactions for the tick.

In Giga there is not a mempool in the traditional sense of the term, there is not a global gossiped collection of transactions for a block producer to select from when building a block, instead each validator is sent transactions directly, which through random tx assignment to a validator has the benefit of allowing for censorship resistance when a tx is known by multiple concurrent validators. A validator can maintain a local mempool for their own purposes but if a tx is known by other validators then the utility of that tx will go to 0 if they fail to have it included in at least the same cut as another validator does.

The random assignment of transactions makes spamming a given leader difficult, unlike in Solana, but means that validators creating blocks concurrently may not have the same set of transactions from which to build their block. As a result, once a validator publicly commits to a block containing their transactions, another validator may take the opportunity to steal txs from the block, or to use the content of that block to attempt to extract extra revenue from their own block.

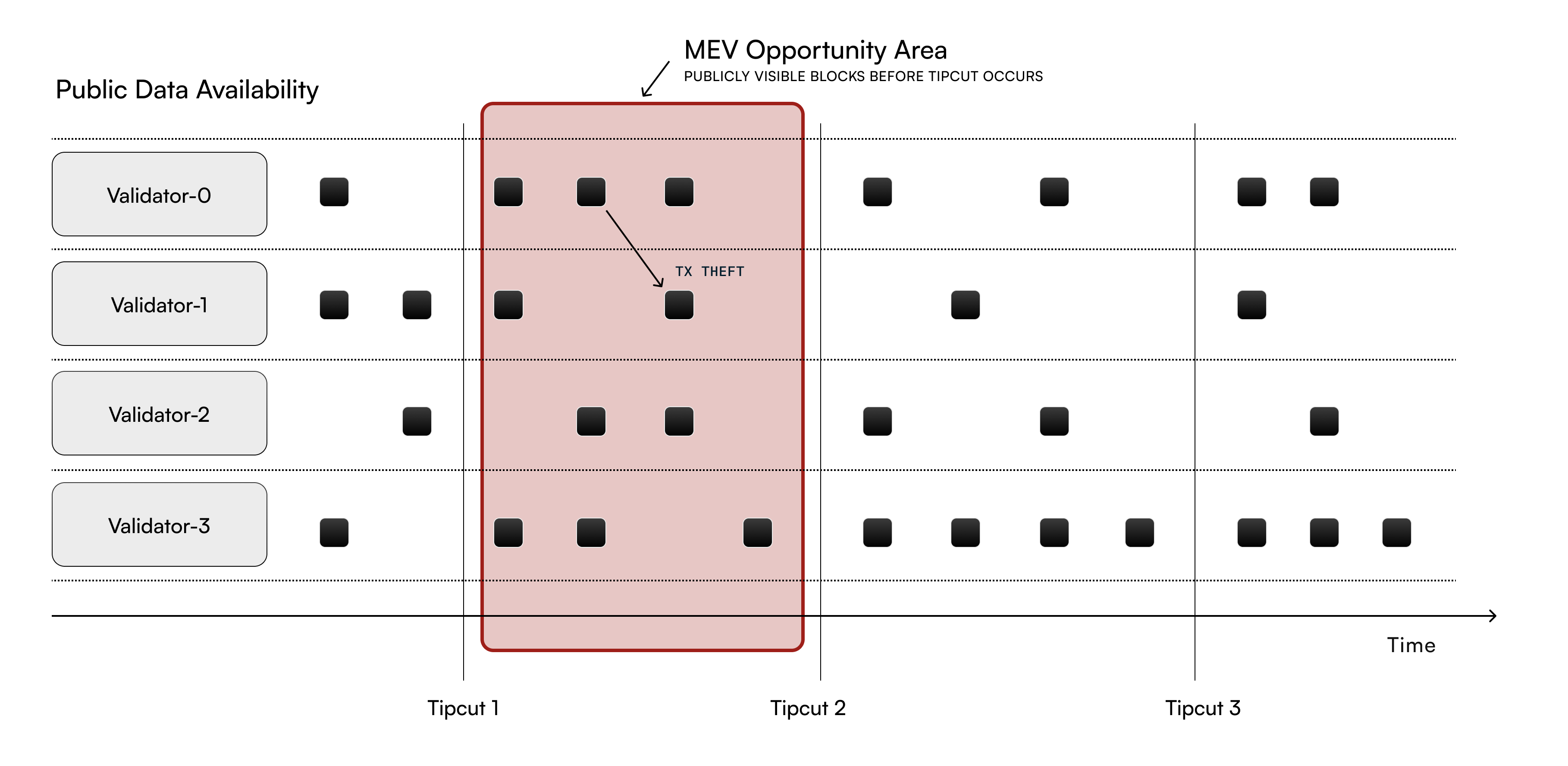
During the vulnerable window highlighted in red, validators can see each other’s proposed blocks before the tip cut finalizes ordering. This creates opportunities for transaction theft and MEV extraction as validators can copy high-value transactions or optimize their blocks based on others’ visible content.

Last look

Last look refers to the ability of a block producer to see the actions of others, and in the case of Autobahn the content of their blocks, before making their own action allowing for them to rationalise their strategy more fully and act at the last moment. The idea exists in TradFi trading but applies directly to MCP.

MEV and transaction theft

In Autobahn the public DA layer shifts how MEV works though many of the traditional concepts still apply. Once a full block is published the content of that block is now exploitable. The validator can steal a tx to extract revenue directly, either from the tip or fee, TFM dependent, or from the ability to exploit that tx for MEV. The validator can also perform inter-block MEV where the validator, or a cartel of validators, attempts to front-run, back-run, or sandwich entire blocks, or the transactions within those blocks indirectly.

Inter-block MEV

More formally we let \(\mathcal{B}(t)=\{B_i\}\) be the set of blocks published at tick \(t\) (but not yet ordered by the tip cut). Each block \(B_i\) carries a multiset of data chunks \(d\in\mathcal{D}(t)\) with associated fee \(f(d)\) and potential arbitrage profit \(v(d)\). A validator \(v_j\) who publishes a competing block \(B_j\) after seeing some \(B_i\) can:

1. Front-run across blocks: insert a high-fee chunk \(d_{\mathrm{front}}\) ahead of a known arbitrage chunk \(d^\ast\in B_i\) to capture price impact.
2. Back-run across blocks: append a chunk \(d_{\mathrm{back}}\) immediately after \(d^\ast\) to capture the residual price movement.
3. Sandwich attack: combine both—front-run and back-run—a high-value trade originally included in another validator’s block.

The proposer’s utility becomes

\[ U(B_j \mid B_i) \;=\; \sum_{d\in B_j} f(d) \;+\;\sum_{d\in B_j\cap\{d_{\mathrm{front}},\,d_{\mathrm{back}}\}} v(d), \]

and the inter-block MEV gain from last look is

\[ \Delta_{\mathrm{MEV}} \;=\; \max_{B_j} U(B_j\mid B_i) \;-\; \max_{B_j} U(B_j), \]

where the first term optimizes \(B_j\) after observing \(B_i\), and the second term is the blind optimal block. In practice this is implemented by MEV searchers broadcasting candidate chunks directly to high-throughput relays or even colluding with proposers to ensure their MEV bundles slot in after observed blocks.

Transaction Theft

Whereas MEV reorders new chunks, transaction theft outright copies a pending chunk from another validator’s block:

• A validator sees a chunk \(d_{\mathrm{orig}}\) in some block \(B_i\) with a high expected payoff (e.g. a flash-loan arbitrage).
• They create a duplicate chunk \(d_{\mathrm{copy}}\) but attach a slightly higher fee \(f(d_{\mathrm{copy}}) > f(d_{\mathrm{orig}})\).
• Because both \(d_{\mathrm{orig}}\) and \(d_{\mathrm{copy}}\) live in the public DA layer, the tip-cut will include whichever yields higher fee—i.e. the thief’s copy—and drop or invalidate the original.

This “DA robbery” yields direct profit for the dishonest validator at the expense of the originator, discouraging users from broadcasting novel or complex strategies. One can formalize the expected steal probability as a function of fee gap \(\delta = f(d_{\mathrm{copy}})\!-\!f(d_{\mathrm{orig}})\) and network propagation delays; but the core insight is that exposing full transaction payloads on DA makes every profitable transaction a potential free-for-all.

Mitigations

Most of the obvious approaches to solving the public DA problem are based around the use of cryptography to allow for an encrypted DA layer.

Commit-reveal schemes

Commit-reveal schemes aren’t new or novel in any real sense but appear at first glance to be the perfect solution to a public DA problem. The idea is to first broadcast a commitment, such as an encrypted block, then to reveal the un-encrypted block later when it is safe to do so. In such a protocol an encrypted block could be published, PoA’s gathered on the existence of the encrypted block, then at the last moment when nobody else has time to act the original block can be revealed.

There are two obvious downsides of this, what if fake blocks are published and what if the block isn’t revealed. Like most crypto, the solution once again appears to be economic, slash validators who publish spam encrypted blocks and slash when a validator refuses to reveal. But what happens if the validator has an economic incentive not to reveal? Doing so would cost them more than being slashed would?

Threshold crypto

Another approach to avoiding a single validator being able to shirk their reveal responsibility would be to distribute that responsibility through a threshold scheme where the decryption key is split over \(m\) validators, requiring no fewer than \(n\) key holders to cooperate to publish the plain text block required for consensus. In such a model the public block is guaranteed assuming an honest threshold of key holders, but relies on key holder liveness to work. A cartel of key holders is still able to prevent the block being released and the messaging overhead from such a protocol would impact performance of the chain.

Timelock crypto

Timelock crypto and VDFs offer an alternative without the need of committees. A VDF is a sequentially hard function V(x) that produces an output and short proof only after a prescribed delay \(\Delta\):

\[ y,\;\pi \;=\; V_{\Delta}(x) \]

such that verifying \((y,\pi)\) is fast, but computing \(y\) from \(y\) requires real time \(\Delta\). Such a protocol would mean anybody can decrypt the committed block but not until some time has passed. The \(\Delta\) latency however may be significant with a chain running at capacity which for Giga is circa 250k TPS meaning even a 500ms delay means a 100k+ backlog to clear. Timelock protocols also tend to cause arms races to attempt to decrypt the block sooner than anyone else giving the attacker a small advantage, avoiding such arms races requires specialized hardware such as ASICs.

In a protocol with ASIC VDFs being run by watchtowers the protocol would enforce economic incentives for the validator to reveal the block immediately ensuring no overhead in the consensus process but watchdogs that can reveal the block eventually ensure a guarantee of the block being public once it is committed to. Such a protocol would be a hybrid protocol taking advantage of the fact that timelock crypto on a ASIC approaches a point where it cannot be optimized further with economic incentives for honest behavior. Such a protocol relies on honest watchdogs existing however.

Future work

We’re actively working on both the public DA problem and a formalization of MEV in this context. We invite developers, researchers, and community members to join us in this mission. This is an open invitation for open source collaboration to build a more scalable blockchain infrastructure. Check out Sei Protocol’s documentation, and explore Sei Foundation grant opportunities (Sei Creator Fund, Japan Ecosystem Fund). Get in touch - collaborate[at]seiresearch[dot]io